환의 종류 | (2022-06-23) |
Commutative Ring, 가환환, Ring with Unity, 단위환, 단위원을 갖는 환, 나눗셈환 | |
▷
Top
▷
기초과학
▷
수학
▷
대수학
▷
추상대수학
▷
환(Ring)
1. 추가적인 조건이 부여됨에 따라 나타나는 또다른 환(Ring)의 형태들 ㅇ 가환환 (Commutative Ring) - 추가적으로 곱셈(·)에 대해서도 가환(commutative)이 되는 환 : a·b = b·a . 즉, 곱셈에 대해 교환법칙까지도 성립하는 가환환 * 한편, 환은, 굳이 곱셈에 대해 교환법칙 성립을 요구하지 않음 - 例) 정수환,유리수환,실수환,복소수환 등 ㅇ 단위환 (Ring with Multiplicative Unity, Ring with Unity) - 추가적으로 곱셈 항등원. 즉, `단위원을 갖는 환` . 단위원(unity or identity) : 곱셈에 대한 항등원 * 한편, 환은, 굳이 곱셈에 대한 항등원을 요구하지 않음 - 즉, 모든 원소 a ∈ R에 대해, 1·a = a·1 = a 인 1 ∈ R 이 존재하는 환 ※ 例) - Z(정수),Q(유리수),R(실수),C(복소수)들은, 모두 단위원을 갖는 가환환 이나, - N(자연수)는, 덧셈 항등원(0)이 없으므로, 환도 아님 ㅇ 나눗셈환 (Division Ring) - 단위원 1을 갖는 환으로써, 곱셈 역원이 존재하는 환 . 각 원소 a∈R,a≠0에 대해, a·a-1 = a-1·a = 1 ㅇ 정역 (Integral Domain) - 단위원(곱셈 항등원) 1을 갖고, 영 인자(0의 약수)를 갖지 않는, 가환환 ㅇ 유클리드 정역 (Eucleadian Domain) - 정수환,다항식환 처럼 나눗셈 정리가 성립하는 정역 - 원소들 간에 크기(size) 개념이 있는 정역 ㅇ 체 (Field) - 가환환인 나눗셈환 . 단위원을 갖는 가환환으로, . 영이 아닌 모든 원소가 단원(unit,역원이 존재하는 원소)이 되는 경우 ㅇ 사체/비가환체 (Skew Field) - 비가환환인 나눗셈환 2. 환, 가환환, 단위환, 정역, 체의 비교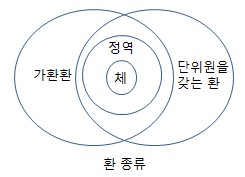
▷환(Ring)
1. 환(Ring) 2. 환의 종류 3. 환 용어 4. 정수 환 5. 다항식 환 6. 정역