Directional Derivative 방향 도함수, 방향 미분계수 | (2022-07-07) |
방향성 미분 | |
▷
Top
▷
기초과학
▷
수학
▷
해석학(미적분 등)
▷
미분적분
▷
미분
▷
다변수함수 미분
1. 방향 도함수 / 미분계수 / 방향성 미분 (Directional Derivative) ㅇ 다변수 함수에서, 방향에 따른 변화율을 계산할 수 있게 해주는, 편도함수의 일종 - 어떤 점에서 임의 방향으로 다변수 함수의 순간 변화율 계산에 편리한 수단 2. 방향 도함수 또는 기울기 벡터 ㅇ 점 (x,y)에서 단위 벡터 u = (u1,u2) 방향으로의 방향 도함수는, - Du f(x,y) = fx(x,y) u1 + fy(x,y) u2 = ∂f(x,y)/∂x u1 + ∂f(x,y)/∂y u2 = ∇f(x,y)·u . Du f : 다변수 함수 f의 방향 도함수 .. 임의 방향 u에 대한 다변수 함수 f의 방향 도함수(순간 변화율) . fx,fy : 편도함수 .. x,y 축방향으로의 편도함수는 일반화된 방향도함수의 특별한 경우 임 . ∇f(x,y) : 기울기 벡터 (∇ : 경도 연산자) .. 함수의 각 점 마다 최대 변화율을 지향하는 벡터 . u : 단위 벡터 .. 방향 도함수의 계산을 특정 방향으로 구하고자 할 때, 그 방향의 단위 벡터 ㅇ 의미 - 벡터 u 위에 기울기 벡터 ∇f를 정사영 시킨 것이, - u 방향으로의 함수 f의 변화율(방향도함수)와 같음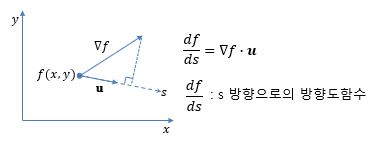
▷다변수함수 미분
1. 전 미분 2. 편 미분 3. 방향 도함수 4. 등위 선/면