Bravais Lattice, 14 Bravais Crystal System Bravais 결정계, Bravais 격자, Bravais 14개 결정계 | (2020-06-04) |
브라베 격자 | |
▷
Top
▷
공학 (역학,기계,재료등)
▷
재료공학
▷
결정학
▷
결정 구조 표현
1. Bravais 14개 결정계 ㅇ `7 결정계` 및 `격자점 위치 구분 4가지 방식`을 결합시켜, - 실존 가능한 결정구조 형태를 14개로 규격화 (1850년)* Auguste Bravais(1811~1863) : 프랑스 결정학자 2. 14개 결정계 구분 방식 ㅇ 입방체,정육면체 (立方, Cubic) : (a=b=c, α=β=γ=90˚) - 단순 입방 (simple cubic,sc) - 면심 입방 (face-centered cubic,fcc) - 체심 입방 (body-centered cubic,bcc)
ㅇ 육방정 (六方, Hexagonal) : (a=b≠c, α=β=90˚,γ=120˚) - 단순 육방정 (simple hexagonal)
ㅇ 정방정 (正方, Tetragonal) : (a=b≠c, α=β=γ=90˚) - 단순 정방정 (simple tetragonal) - 체심 정방정 (body-centered tetragonal)
ㅇ 삼방정 (三方, Rhombohedral,Trigonal) : (a=b=c, α=β=γ≠90˚) - 단순 삼방정 (simple rhombohedral)
ㅇ 사방정 (四方 또는 斜方, Orthorhombic) : (a≠b≠c, α=β=γ=90˚) - 단순 사방정 (simple orthorhombic) - 체심 사방정 (body-centered orthorhombic) - 면심 사방정 (face-centere orthorhombic) - 저심 사방정 (base-centered orthorhombic)
ㅇ 단사정 (單斜, Monoclinic) : (a≠b≠c, α=γ=90˚,β≠90˚) - 단순 단사정 (simple monoclinic) - 저심 단사정 (base-centered monoclinic)
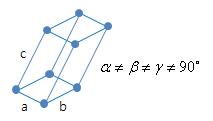
ㅇ 삼사정 (三斜, Triclinic) : (a≠b≠c, α≠γ≠β≠90˚) - 단순 삼사정 (simple triclinic)
▷결정 구조 표현
1. 결정 구조 2. 결정계 (7 결정계,4 결정계) 3. Bravais 결정계 4. 밀러 지수 5. 결정 대칭