Finite Field, Galois Field, Galois Finite Field 유한체, 갈로아체, 갈로이스체, 갈로아 유한체 | (2023-12-30) |
Galois Theory, 갈로아 이론, 이진 유한체, 이진체 | |
▷
Top
▷
기초과학
▷
수학
▷
대수학
▷
추상대수학
▷
체(Field)
1. 유한체 (Finite Field) ㅇ 유한개 원소 만을 갖고, 그 안에서 대수적 구조를 형성하는 체 ☞ 체(Field) 참조 - 즉, 유한체 집합 내 원소의 연산(덧셈,곱셈 등) 결과가, 다시 그 집합 내에 있게됨(닫힘성) ㅇ 유한체를 `갈로이스체(Galois Field)` 라고도 불리움 - 갈로아 이론 : 체의 대칭성 구조를 군의 구조로 바라다볼 수 있게 한 이론 * 갈로이스(Pierre Galois 또는 Evariste Galois, 1811-1832) : 프랑스 수학자 ㅇ 특히, 코드(부호) 등을 기술하는데 유용한 수학적 `대수 구조 (Algebraic Structure)`를 갖음 - 유한체는 부호화 이론, 암호학 등에서 많이 응용되는 `대수적 구조`임 . 실수체 R, 복소수체 C 등은 그 요소 수가 무한 개인 무한 체이나, . 갈로이스체는 유한체(Finite Field)라고해서 그 요소 수가 유한(제한)개임 2. 유한체의 표기 ㅇ q개의 원소를 갖는 유한체 표기 - GF(q) 또는 Fq 또는 GF(pn) 또는 (Fq)n 또는 Fqn ㅇ {#GF(p^n)#} : q = pn개의 유한개 원소를 갖는 유한체(Galois체) - q : 위수 (位數, Order : 유한 체 내 원소의 갯수) . 유한개 원소 수 : pn = q 개 (0 포함) . [참고] 유한 체의 원소 수는, .. 소수 또는 소수의 멱(prime power) 만 가능하다고, 갈로이스가 밝힘 . 즉, 유한체의 크기(원소 수)는, 항상 소수 p(표수)의 거듭제곱(pn) 형태 임 - p : 표수 (標數, Characteristic). 때론, 기수(base)라고도 함 . 유한체는, 항상 양의 표수 p를 갖음 . 여기서, p가 소수이면, 이를 소수체(Prime Field)라고 함 - n : 양의 정수 (dimension) - GF(q) : 위수(order) q를 갖는 유한체 3. 유한체의 위수/길이/차수 (Order) q (유한체 중요 성질 임) ㅇ 원소의 개수가 항상 소수(p)의 거듭제곱(pn=q)이 됨 (갈로이스가 밝힘) - 例) GF(5),GF(8) => 유한체 존재함 - 例) GF(6),GF(10) => 유한체 존재 안함 ㅇ 전영(0) 원소를 뺀 나머지 원소들은, 순환 군(Cyclic Group)을 이룸 4. 유한체의 표현 例) ※ 유한체는, - 비록, 다른 연산 형식도 가능하나, - 주로, 아래와 같이 모듈러 연산에 적용시켜 표현하는 경우가 많음 ㅇ GF(2) 또는 ( {0,1}, +, x ) - 21=2개의 유한개 원소 {0,1}를 갖는, 단순 2진 유한체 (binary field)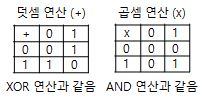
- 성질 . (정수 modulo 2)의 환(Ring)과 같음 ㅇ GF(2n) 또는 {#F^n_2#} : 대부분 응용에 사용되는, 2진 부호화 형식이 이 형태를 취함 - `0`,`1` 2개 요소의 n-tuple로써 이루어진, n 튜플 2진 유한체 (n-tuple binary field) . 2n개(위수,位數 : pn = q)의 유한개 원소들이, 어떤 벡터공간을 생성(Span)함 . {0,1} 즉, 2개의 기수(base)로써 구성되는, 2진 n-tuple 로써 표현 가능
* 例) (7,4) 해밍코드에서, 부호화(매핑)에 대해, 유한체에 의한 수학 기호 표현은, . f : GF(24) → GF(27) ㅇ GF(3) - 3개의 유한개 원소 {0,1,2}를 갖는 3진 유한체 (ternary field)
- 성질 . (정수 modulo 3)의 환(Ring)과 같음 ㅇ GF(4) - 4개의 유한개 원소 {0,1,β,β2}를 갖는 4진 유한체 (quaternary field)
- 성질 . (정수 modulo 4)의 환(Ring)과 같지 않음 . x + x = 0, β2 = β + 1, β3 = 1, . β4 = β2β2 = (β + 1)(β + 1) = β2 + β + β + 1 = β 5. [참고사항] ㅇ 체의 확대 (field extension) ☞ 부분체, 확대체 참조 ㅇ 체 용어 ☞ 원시 원소 (Primitive Element) 참조 ㅇ 부호화 이론에서 유한체의 응용 (에러정정코드) 例) ☞ BCH 부호, RS 부호, LDPC 등
▷체(Field)
1. 체(Field) 2. 체(Field) 용어 3. 유한체, 갈로아체 4. 유한체 성질