Polynomial Interpolation 다항식 보간법 | (2023-06-02) |
보간 함수, 보간 다항식, Newton 보간법 | |
▷
Top
▷
기초과학
▷
수학
▷
수치해법
▷
곡선적합 (근사)
1. 보간 함수, 보간법 ㅇ 보간 함수 (Interpolation Function) - 구간 내 주어진 특정 점들을 통과하는 함수 ㅇ 보간법 (Interpolation Method) - 구간 내 특정 점들을 지나는 함수 및 그에따른 함수 값을 구하는 방법 2. 보간 다항식, 다항식 보간법 ㅇ 보간 다항식 (Interpolation Polynomial) - 보간 함수를 근사시키는 다항식 - 즉, 보간점(interpolation point)들을 지나는 다항식 . 1차 보간 다항식 : 두 점 연결 (선형 보간) . 2차 보간 다항식 : 세 점 연결 (포물선 보간) . 3차 보간 다항식 : 네 점 연결 (3차 곡선 보간) ㅇ 다항식 보간법 - 구간 내 데이터점을 모두 지나는 보간 다항식을 구하는 방법 . 구간 전체에 대해 하나의 다항식으로 근사화 . 보간점 개수가 커짐에 따라 다항식 차수가 매우 커짐(계산량,변동폭도 커짐) . n개의 데이터점 간의 보간을 위해 (n-1)차 다항식을 유도함 3. 선형 보간법 (Linear Interpolation) ㅇ 가장 간단한 보간법으로써, 2개 점을 지나는 직선에 의해 구해짐 . f(x) = a0 + a1x 4. 테일러 다항식 (Taylor Polynomial) 보간법 ㅇ 특정 한 점에서 만 매우 잘 근사함 - 구간 전체에 고른 근사를 필요로하는 보간법에 적용하기는 부 적합함 5. Newton 보간법 (Newton's Interpolatory Divided Difference Interpolation) ㅇ 분할 차분(Divided Difference)의 선형 조합으로 미지 함수를 묘사 - 테일러 다항식과 유사 * 테일러 다항식 : 기지의 함수 및 도함수들의 선형 조합으로 미지 함수를 묘사 ㅇ 차분, 분할 차분 이란? - 차분(Difference) : 임의 두 점에서의 함수값들의 차이 - 분할차분(Divided Difference) : 분할구간에서 함수값들의 차이 ㅇ 분할 차분 - 0차 분할차분 : 주어진 점이 1개 - 1차 분할차분 : 주어진 점이 2개 - 2차 분할차분 : 주어진 점이 3개 - k차 분할차분 : 주어진 점이 (k+1)개6. Lagrange 보간 다항식 보간법
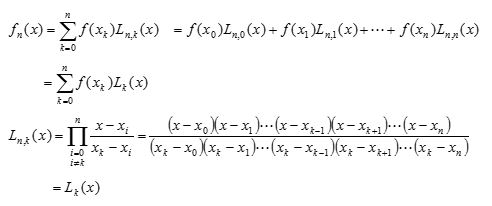
▷곡선적합 (근사)
1. 곡선적합(Curve Fitting) 2. 보간법 3. 선형 보간법 4. 다항식 보간법 5. 스플라인 보간법 6. 최소자승법 7. 회귀분석