Curvature, Radius of Curvature   곡률, 곡률반경

1. 곡률 및 곡률반경

  ㅇ 곡률(Curvature) K                    = (원 반지름 또는 곡률 반경)의 역수 = 1/r  
     - 휘어진 정도
        . 얼마나 급격하게 굽혀졌는가의 척도
       
        . 작은 원 형태일수록 곡률은 커짐
        . 큰 원 형태일수록 곡률은 작아짐

  ㅇ 곡률 반경(Radius of Curvature) r     = 곡률의 역수 = 1/K
     - 구면(球面,곡률원) 일 때의 그 반지름을 말함


2. 곡률 응용

  ㅇ [케이블]  허용 반경  ☞ 케이블 곡률반경 참조

  ㅇ [렌즈]  파면 곡률 단위 또는 버전스 단위
     -  [m-1] 또는 디옵터 [D] 또는 [Dptr]  ☞ 버전스(Vergence) 참조


3. [미분 기하학]  곡률 정의

  ㅇ 굴곡있는 곡선 상의 한 점에서 곡률 정의
      
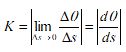     - Δθ : 두 인접 점 간의 접선각의 변화량
     - Δs : 두 인접 점 간의 호의 길이

  ㅇ 복잡한 곡률 계산에 대한 간편식 (극좌표)
     

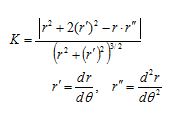  ㅇ 기울기(곡선길이방향의 1차 도함수)가 얼마나 빨리 변화하는가를 나타내는 변화율
     - 곡선을 따라 변화하는 단위길이당 변화율 즉, 2차 도함수