Pulse 펄스 | (2025-01-30) |
Pulse Wave, 펄스파, Square Wave, Square-wave, 구형파, Rectangular Wave, 직사각파, Rectangular Pulse Wave, 사각 펄스파, 사각파, Rectangular Function, 직사각형 함수 | |
▷
Top
▷
전기전자공학
▷
신호 및 시스템
▷
신호 표현/성질
▷
신호 파형 종류
1. 펄스 (Pulse) 이란?
ㅇ 펄스 (Pulse)
- 짧은 시간 동안 만 존재하는 일련의 파동(전기 흐름,진동 현상 등)
ㅇ 펄스 파형 (Pulse Wave)
- 일반적으로, 여러 모양(계단함수파,지수함수파,램프함수파,삼각파 등)을 갖지만,
. 보통은, 단 하나의 골과 마루를 갖는 파형을 주로 칭함
- 다만, 통상적인 전기적인 펄스 파형으로는,
. 임의 레벨로 수직 상승하였다가 상승한 레벨을 일정 시간 유지하다가,
. 다시 하위 레벨로 수직 하강하는 직사각 파형을 주로 말함
2. 구형파 (矩形波,square wave) 또는 직사각파 (直四角波,rectangular wave), 사각 펄스파
ㅇ 시간 영역에서 직사각형 모양을 하는 신호 파형
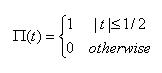
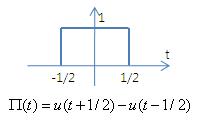
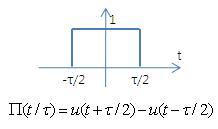 ㅇ 표기 : 크기 A, 펄스폭 τ 이면 => A ∏(t/τ) 또는 A Rect(t/τ)
ㅇ 명칭 : 통상, 주기적으로 반복하는 경우에,
- 반복 구형파는, 시간간격이 규칙적인 것을 지칭하고,
- 반복 직사각파는, 시간간격이 일정하지 않은 것을 지칭
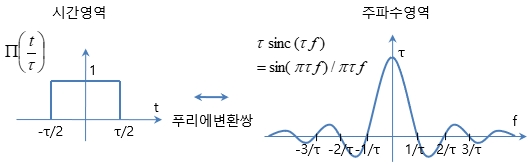
3. 펄스파의 주파수 영역(푸리에변환) 표현
ㅇ 주파수 영역 상에서, 정현파의 기본파 및 모든 기수 고조파가 합해진 형태이며,
ㅇ 이는, Sinc 함수의 모양을 나타냄
- 즉, 고조파 차수가 높아질수록,
- 진폭은 점차 작아지며,
- 균등 위상 차이가 나는 형태를 지님
[# \Pi \left(\frac{t}{τ}\right) = \text{rect} \left(\frac{t}{τ}\right)
= u\left(t+\frac{τ}{2}\right) - u\left(t-\frac{τ}{2}\right)
\;\; \leftrightarrow \;\; τ\;\text{sinc}(πτf) = τ\;\frac{\sin{(πτf)}}{πτf} #]
ㅇ 표기 : 크기 A, 펄스폭 τ 이면 => A ∏(t/τ) 또는 A Rect(t/τ)
ㅇ 명칭 : 통상, 주기적으로 반복하는 경우에,
- 반복 구형파는, 시간간격이 규칙적인 것을 지칭하고,
- 반복 직사각파는, 시간간격이 일정하지 않은 것을 지칭
3. 펄스파의 주파수 영역(푸리에변환) 표현
ㅇ 주파수 영역 상에서, 정현파의 기본파 및 모든 기수 고조파가 합해진 형태이며,
ㅇ 이는, Sinc 함수의 모양을 나타냄
- 즉, 고조파 차수가 높아질수록,
- 진폭은 점차 작아지며,
- 균등 위상 차이가 나는 형태를 지님
[# \Pi \left(\frac{t}{τ}\right) = \text{rect} \left(\frac{t}{τ}\right)
= u\left(t+\frac{τ}{2}\right) - u\left(t-\frac{τ}{2}\right)
\;\; \leftrightarrow \;\; τ\;\text{sinc}(πτf) = τ\;\frac{\sin{(πτf)}}{πτf} #]
 4. [참고사항]
ㅇ (변조) 펄스파에 의한 변조 ☞ 펄스 변조
- 주기적인 펄스를 정보 신호에 의해 변조하는 방식
ㅇ (발생) 펄스 파형의 발생 ☞ 펄스 파형 발생기(비안정 멀티바이브레이터)
- 펄스파 열(Pulse Train)의 발생, 일련의 펄스파 발생
ㅇ (부호화) 2진 비트 열(列)과 전기적인 펄스 신호가 직접 대응되는 부호화 ☞ 선로 부호
ㅇ (레이더) ☞ 레이더 펄스 참조
4. [참고사항]
ㅇ (변조) 펄스파에 의한 변조 ☞ 펄스 변조
- 주기적인 펄스를 정보 신호에 의해 변조하는 방식
ㅇ (발생) 펄스 파형의 발생 ☞ 펄스 파형 발생기(비안정 멀티바이브레이터)
- 펄스파 열(Pulse Train)의 발생, 일련의 펄스파 발생
ㅇ (부호화) 2진 비트 열(列)과 전기적인 펄스 신호가 직접 대응되는 부호화 ☞ 선로 부호
ㅇ (레이더) ☞ 레이더 펄스 참조
▷신호 파형 종류
1. 정현 신호 2. 지수 신호 3. 삼각 함수 4. 계단 신호 5. 램프 신호 6. 임펄스 신호 7. 삼각 펄스 신호 8. 구형 펄스 신호 9. 싱크 신호 10. 특이 함수 11. 기초 이산 신호 12. 복소 지수 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]